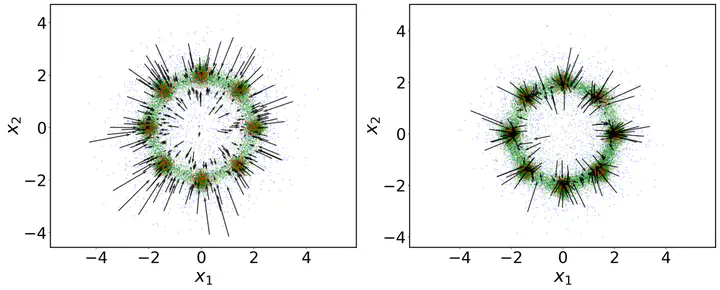
Comparison of the denoising field early in the diffusion process for Gaussian vs. fat-tailed noise. Denoising posterior in green, true distribution in red, noisy samples in blue.Abstract
Denoising and score estimation have long been known to be linked via the classical Tweedie’s formula. In this work, we first extend the latter to a wider range of distributions often called “energy models” and denoted elliptical distributions in this work.
Next, we examine an alternative view: we consider the denoising posterior $P(X|Y)$ as the optimizer of the energy score (a scoring rule) and derive a fundamental identity that connects the (path-) derivative of a (possibly) non-Euclidean energy score to the score of the noisy marginal.
This identity can be seen as an analog of Tweedie’s identity for the energy score, and allows for several interesting applications; for example, score estimation, noise distribution parameter estimation, as well as using energy score models in the context of “traditional” diffusion model samplers with a wider array of noising distributions.
In this work, we (among other things):
- Extend Tweedie’s identity beyond the exponential family to a broad class of noising distributions, often called energy models (which we denote as elliptical distributions to avoid confusion, see below).
- Derive a fundamental identity connecting the Stein score of the noisy marginal to the (path-) derivative of the energy score, a scoring rule. Despite the similarity of the names, these concepts had not been connected before to the best of our knowledge.
- Propose a practical score estimation approach based on this identity, using samples from the denoising posterior.
- Introduce a generative modeling procedure that uses energy-score-based posterior models within classical diffusion-style sampling with a wide range of noising distributions; among other things, this enables a principled way of doing heavy-tailed diffusion.
The Stein score previously appeared in connection with an energy score model in Distributional Autoencoders Know the Score; however, the setting here is denoising, while the former dealt with the optimal encoding of “clean” data by an autoencoder.
