Distributional Autoencoders Know the Score
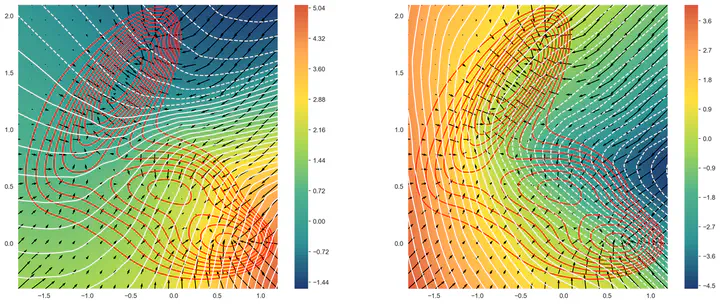The encoding for the Müller-Brown potentialAbstract
The Distributional Principal Autoencoder (DPA) combines distributionally correct reconstruction with principal-component-like interpretability of the encodings. In this work, we provide exact theoretical guarantees on both fronts. First, we derive a closed-form relation linking each optimal level-set geometry to the data-distribution score. This result explains DPA’s empirical ability to disentangle factors of variation of the data, as well as allows the score to be recovered directly from samples. When the data follows the Boltzmann distribution, we demonstrate that this relation yields an approximation of the minimum free-energy path for the Müller–Brown potential in a single fit. Second, we prove that if the data lies on a manifold that can be approximated by the encoder, latent components beyond the manifold dimension are conditionally independent of the data distribution - carrying no additional information - and thus reveal the intrinsic dimension. Together, these results show that a single model can learn the data distribution and its intrinsic dimension with exact guarantees simultaneously, unifying two longstanding goals of unsupervised learning.
For a recently introduced class of autoencoders, we prove that:
the encoder level sets align exactly with the data score in the normal directions, and
extra latent dimensions beyond the data manifold become completely uninformative, revealing the intrinsic dimension.
These hold simultaneously and circumvent the usual reconstruction/disentanglement trade-off in unsupervised learning.
The first result also leads to strong performance on molecular simulation data: when the data follow a Boltzmann distribution, the learned encoding aligns with the (unknown) force field, allowing the method to recover an approximation of the minimum free-energy path for the Müller–Brown potential in a single fit, with the potential to speed up chemical simulations.
Thus, we extend the analogy to PCA made in the original DPA work by proving that, instead of finding principal linear subspaces, DPA learns nonlinear manifolds shaped locally by the data density, with a clear, testable dimensionality criterion — conditional independence.
